Клоунът Сергеев, който всички познавали с името Мусля, по време на турне в Сибир бил в същият хотел, в който бил отседнал известен цигулар, пристигнал за първи път на това място. Техните стаи се оказали една до друга.
Музикантът рано сутринта репетирал ново сложно произведение, а вечерта, за да се разведри отишъл на цирк, неговият концерт щял да бъде едва след два дена.
Сложили го на първия ред. На арената излязъл Мусля със стара цигулка и изпълнил три музикални импровизации.
Слушателите затаили дъх, той свирел майсторски.
Гастролиращият цигулар чул фрагменти от произведение нотите, на които били у композитора-автор и музиканта, за който била написана тази музика.
Известният музикант се втурнал зад кулисите:
– От къде взехте тази музика?
– Тази сутрин в хотела, – искрено признал Мусля, – някой свиреше в хотела. Хареса ми мелодията и я запомних.
– Вие сте гений. Това е невероятно. Да запомните и да изсвирите тази музика по памет. Нужно е да се опознаем по-отблизо.
След спектакъла цигуларят в модерен костюм и много по-скромно облечен клоун отишли в един ресторант.
Три дена след това Мусля отсъствал от цирка, а концертът на цигуларят трябвало да се отмени. Нито музиканта, нито клоуна могли да намерят.
А те се затворили в една стая, изключили телефоните си и свирели един на друг. Когато свирел известният цигулар плачел Мусля, а когато свирел Мусля, плачел цигуларят.

Седяха на масата и започнаха да се изучават взаимно. Нямаше много хора и обстановката предразполагаше към откровен разговор.

– Хайде да поръчаме шампанско! – усмихна се приветливо Мартин.

– Две чаши шампанско, моля. Силно газирано, без пяна и достатъчно студени., – каза Милена на келнера, когато той дойде да приеме поръчката.

Мартин едва удържа усмивката си. След каро сервитьорът се отдалечи разговорът се възобнови.

– Разкажете ми за големия мъж, за който сте се оженила, – каза Мартин. – Чух, че доста е пораснал в една  чуждестранна инвестициозна банка.

– Какво да ти кажа, той наистина много се старае. Господар е на една юридическа джунгла.

Тя усети присмехулния му поглед, но се направи, че не го забелязва. Мартин беше човек работещ за прехраната си, а тя богата бизнес дама, която разполагаше с живота си, както намери за добре.

– Изглежда двамата служим на различни богове, – подкачи я Мартин.

– Аз не служа на нищо и на никого, – нервно подръпна ръкава на блузата си Милена, – аз съм идеологически неутрална.

– Съмнявам се, това да е възможно, – хладни пламъчета пробляснаха в очите на Мартин.

– Но аз не съм вярваща. – вдигна рамене Милена. – Не само не вярвам, но и не проявявам интерес. Мога да си карам чудесно без каквито и да е богове и религии.

– Вие имате религия, – вече съвсем сериозно каза Мартин. – И знаете ли каква е вашата религия?

– Правото! – уверено каза Милена, все пак тя беше и адвокат.

– Не, това е средство за постигане на целите. Вашата религия е редът.

– В какъв смисъл? – недоумяваше Милена

– Това е божеството около което се върти животът ви. Живеете в хаутичната джунгла на финансовото бойно поле, но целият ви живот е посветен на това, да внасяте ред в хауса.

Милена се разсмя:

– Никога не съм чувала подобно нещо.

– Вашата отдаденост на реда се забелязва още във външния ви безупречен вид. Косата ви е винаги добре оформена. Полата и роклята ви никога не са измачкани. Папките, докладите, записките и писмата са блестящо подредени, като войници в строя. Ако успеете да превърнете хауса в ред смятате, че владеете положението. За целта използвате здравия си разум и интелекта си. Така постигате огромен успех в професията си. А какво дава този успех? Пари, власт и положение. Но те са ви необходими за да осигурите по-голям контрол над своя живот, което ви помага да се наслаждавате на реда. Вие сте дълбоко религиозна. Богослуженията ви са часовете прекарани в офиса. Вашата троица са пари, власт и положение, но над всички е редът, основа за съществуването ви, източник на силата ви, вашата любов на живота.

– Искаш да кажеш, че съм смахната?

– В никакъв случай. Просто казвам, че не сте идеологически неутрална и си имате бог.

– Нима хората не обичат реда? Кой не желае да направлява сам живота си?

– Напротив, много хора обичат хауса, намират го дори за стимулиращ. Но до каква степен контролираме живота си, особено ако сме подритнати от някой над когото нямаме власт?

– Някаква степен на организация винаги е възможна. Особено ако човек си състави житейски план….

Мартин звънко се засмя:

– Житейски план?

– Стига само човек да си съствави напълно последователен план, продиктуван от здравия разум и логиката, – настояваше разгорещено Милена, но Мартин продължаваше да се смее. – Няма причина  бъдещето да не бъде поставено под контрол.

– Признавам, че всички се нуждаем от цели, към които да се стремим, но такъв план, какъвто вие предлагате, ще се провали. Бъдещето е непредсказуемо.

– Не и моето, – сви гневно устни Милена.

– Защо толкова се страхувате, – започно по-спокойно Мартин. – Промените и непредвидените неща в бъдещето, дават възможност за изграждане на човека. Като затворите вратата на бъдещето, което не можете да предвидите, ограничавате себе си. Нима не разбирате това? Как Бог би ви отредил вълнуваща роля в сътворението, ако вие смятате сътворението за бъркотия и отказвате да излезете от безупречно подредения си килер?

Всеки от тях вдигна чашата си и отпи, като знак за помирение. След това щяха да се разделят и всеки щеше да поеме по своя избран път.

Иван беше повярвал от скоро. В миналото си е бил алкохолик. Реши и той да се ожени. Предложил на едно момиче от църквата, но то отказа. Предложи на друго и отново получи отказ.
След няколко неуспешни опита съвсем се отчая. Тогава отиде при една жена двадесет години по-голяма от него и ѝ предложи брак.
Тази жена не му се присмя, нито го изгони, а съвсем сериозно прие предложението му. Тя му каза:
– Дошъл си на първата ни среща, а панталоните ти са неогладени, обувките непочистени, а и ризата ти не ухае много приятно. Следващия път се приведи в ред.
На следващата среща Иван беше изгладен, всичко по него блестеше и лъхаше на приятен одеколон.
– Иване, щом искаш да станеш мой мъж, трябва да ме наставляваше по Божието слово. А ти знаеш ли Писанието?
От къде да го знае, нали съвсем скоро е повярвал!
Тогава Радка, така се казваше тази жена, започна всяка седмица да изучава Божието слово с Иван. Когато той постигна определен напредък Радка му каза:
– Иване, аз съм стара. Сега ти знаеш Писанието и как да се подържаш по-добре. Иди предложи сега на някое момиче брак, всяка ще се съгласи да те вземе.
Така и стана. Иван направи предложение на младо образовано момиче и то се съгласи.
Хубаво е, че има такива мъдри жени.

Живели някога двама съседи. Никога не се карали, но постоянно си съперничели.
Една зима паднал дълбок сняг. Първият съсед излязъл рано сутринта с лопата в ръка, за да разчисти снега пред къщата и да направи пътечка към пътя. Погледнал в двора на съседа. Към неговия дом водела старателно почистена пътечка.
На следващата сутрин валяло отново. Първия съсед решил да излезе половин час по-рано. Погледнал към съседа, а към дома му отново води почистена пътечка.
На третия ден виелицата яко вилняла. Сняг бил се нарупал повече, отколкото в предишните дни. Излязъл първия съсед да възстанови реда в двора си на разсъмване. Погледнал в съседния двор, а там пътечката до дома на съседа стои почистена, все едно не е валял сняг.
Изненадан от това първият съсед решил да разбере, как съседа му успява да разчисти пътеката до дома си. В този ден двамата се срещнали на улицата. Като разменили няколко думи за работите си, първия съсед между другото попитал:
– Съседе, кога успяваш да почистиш снега пред дома си, сняг вали почти всеки ден?
Вторият съсед се изненадал от въпроса, но после се засмял и казал:
– Та аз никога не го чистя, просто приятели ми идват често на гости!

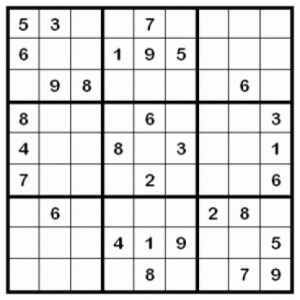В света има много различни, забавни и увлвкателни логически игри. Индия ни е дала шахмата, ханойските кули са измислени от фрески математици, но известната игра Судоку няма определена родина. Прието е да се смята, че тази игра идва от Япония, защото за първи път Судоку в този вид се е появила на страниците на японския вестник.
Независимо от това, историята на тази игра е доста интересна. Безспорно тя принадлежи към класа на математически и логически игри. Смята се, че прародител на Судоку е цял клас задачи, известни като „магически квадрати“. Първите магически квадрати са се появили в Китай преди около 2000 години.
За първи път, нещо напомнящо на Судоку, ще намерим в записките на кралския математик Леонард Ойлер. В архивите на трудовете му, които датират от 17-ти октомври 1776, има записи за математически квадрати и правила за тяхното конструиране в числови клетки 9, 16, 25 и 36. В друг документ, наречен „Научно изследване на нови видове магически квадрат“ Леонард Ойлер е поместил в клетките на магическите квадрати латински букви. Вследствие такива квадрати се наричат Латински. Именно Ойлер е обърнал внимание на проблема с логическото поставяне на знаците, така че във всеки ред и колона да няма повтарящи се символи.
За да получим Судоку в съвремения му вид, трябва да поставим в клетките на магическите квадрати цифри. Това е направил Гарис Харвард през 1979 г. на страниците на американското списание  Word Games. За това на Гарис днес приписват авторството на Судоку, въпреки че в списанието играта се е наричала по друг начин. Като подчертал основния принцип на Латинския квадрат на Ойлер, Гарис добавил и свое условие – символите не трябвало да се повтарят във вътрешните квадрати 3 на 3.
По този начин, можем спокойно да кажем, че в исторически план, играта не идва от Япония, както мнозина мислят. В Япония, тя просто е получила втори живот и модерно име, появявайки се за първи път на страниците на Monthly Nicolist в априлския му брой за 1984 година.